Witaj Marleno, na wstępie przypominam o zaległych pracach. Zgodnie z umową jestem do dyspozycji na komunikatorze.

Temat lekcji: Proste i płaszczyzny w przestrzeni.

Do zeszytu notatka! (podręcznik str. 118)

Prosta to jedno z najważniejszych pojęć geometrii, pierwowzorem matematycznie rozumianej prostej są: linia, która w każdym swoim miejscu wygląda jak naprężona struna w stanie spoczynku, tor swobodnie spadającego przedmiotu, linia zgięcia kartki, promień śwatła, itp. W niektórych ujęciach geometrii prosta jest pojęciem pierwotnym. W innych ujęciach prostą traktuje się jako podzbiory płaszczyzny lub przestrzeni.

Płaszczyzna to jedno z najważniejszych pojęć geometrii, pierwowzorem matematycznie pojmowanej płaszczyzny jest powierzchnia rozłożonej na stole kartki papieru, powierzchnia tablicy, itp. Płaszczyznę traktuje się albo jako pojęcie pierwotne (wtedy jej własności podane są w odpowiednich aksjomatach), albo jako podzbiór przestrzeni.

 Proste i płaszczyzny w przestrzeni

Proste w przestrzeni

Dwie proste w przestrzeni mogą przecinać się, być równoległe lub skośne (wichrowate).

Proste równoległe

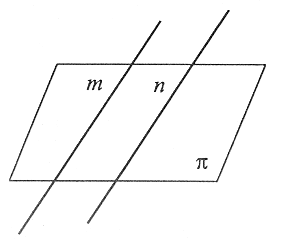Jeśli proste są równoległe, to zawierają się w jednej płaszczyźnie i nie mają punktów wspólnych.

Proste przecinające się

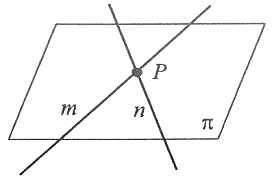Proste przecinające się zawierają się w jednej płaszczyźnie i mają jeden punkt wspólny.

Proste skośne

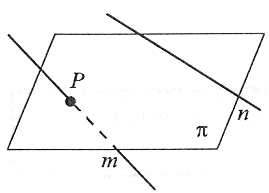Proste skośne nie są zawarte w jednej płaszczyźnie i nie mają punktów wspólnych.

Płaszczyzny w przestrzeni

Dwie płaszczyzny w przestrzeni mogą się przecinać, pokrywać lub być równoległe.

Płaszczyzny przecinające się

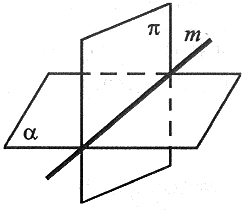Jeżeli dwie płaszczyzny przecinają się, to ich wspólne punkty tworzą prostą, która nazywa się krawędzią przecięcia się płaszczyzn.

Płaszczyzny pokrywające się

α = π   α || π

Płaszczyzny pokrywające się są zaliczane do płaszczyzn równoległych.

Płaszczyzny równoległe

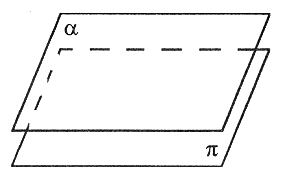Płaszczyzny równoległe nie mają punktów wspólnych (lub pokrywają się).

Odległość dwóch płaszczyzn równoległych

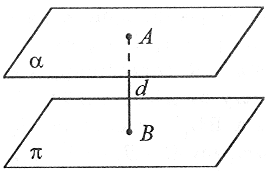d = |AB| AB⊥α   (AB⊥π) A∈α   B∈π

Odległość płaszczyzn równoległych jest to długość odcinka AB prostopadłego do tych płaszczyzn, o końcach A i B, które należą odpowiednio do tych płaszczyzn.

Położenie prostej i płaszczyzn

Prosta może przecinać (przebijać) płaszczyznę, być równoległa lub zawierać się w płaszczyźnie (szczególny przypadek równoległości).

Prosta przecinająca płaszczyznę

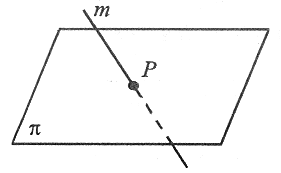P∈m   i   P∈π

Prosta przecinająca płaszczyznę ma z tą płaszczyzną dokładnie jeden punkt wspólny.

Prosta równoległa do płaszczyzny

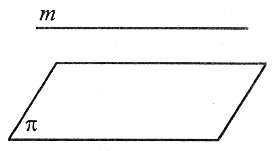m ||π

Prosta równoległa do płaszczyzny nie ma z płaszczyzną żadnych punktów wspólnych lub zawiera się w tej płaszczyźnie.

Prosta zawierająca się w płaszczyźnie

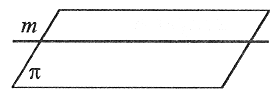m∈π	Prostą zawierającą się w płaszczyźnie zaliczamy do prostych równoległych do tej płaszczyzny.

Prosta prostopadła do płaszczyzny

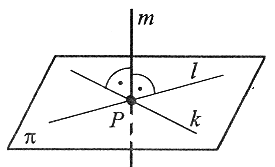m⊥k,   m⊥l   oraz   m⊥π

Prosta m przecinająca płaszczyzne π w punkcie P jest prostopadła do płaszczyzny π, jeśli jest ona (m) prostopadła do każdej prostej zawartej w płaszczyźnie π i przechodzącej przez punkt P.

Rzut prostokątny

Rzut prostokątny punktu na płaszczyznę

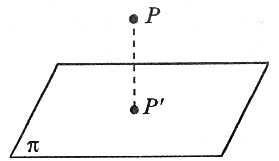Rzutem prostokątnym punktu P na płaszczyznę α nazywamy punkt P’, w którym prosta przechodząca przez punkt P i prostopadła do płaszczyzny α przecina tę płaszczyznę.