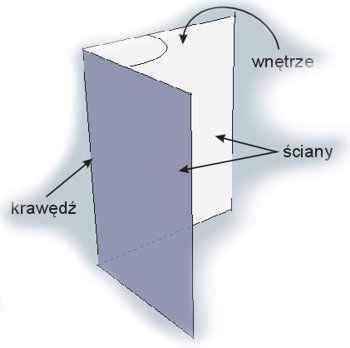
Kątem dwuściennym nazywamy – jak wskazuje sama nazwa – kąt między dwoma (sąsiadującymi ze sobą) ścianami

.

Procedura wyznaczania kąta dwuściennego jest następująca:

– najpierw musimy dysponować dwoma sąsiadującymi ze sobą ścianami (mogą to być np.: ściany boczne w graniastosłupie, ściana boczna graniastosłupa oraz jego podstawa, ściana boczna ostrosłupa oraz jego podstawa, itd.);

– ściany te przecinają się – a zatem możliwe jest wskazanie prostej powstałej poprzez przecięcie tych ścian – wyróżniamy ją;

– na obydwu ścianach (a zatem płaszczyznach) wyróżniamy proste (półproste) prostopadłe do wskazanej prostej (patrz rysunek);

– kątem dwuściennym nazywamy kąt pomiędzy tymi wyróżnionymi prostymi (półprostymi).

Uwaga:

Wyróżnione przez nas proste (półproste) tworzą tak naprawdę dwa kąty. Jednym z nich jest kąt dwuścienny wypukły, drugim – kąt dwuścienny wklęsły.

Kątem dwuściennym wypukłym będzie kąt o mierze mniejszej niż 180 stopni:

Kątem dwuściennym wklęsłym jest ten kąt, który ma miarę większą niż 180 stopni a zatem znajduje się „po drugiej stronie” kąta wypukłego:

 

Przykład:

Kątem dwuściennym nie będzie kąt wyznaczony w oparciu o proste (półproste), które nie są prostopadłe do prostej będącej przecięciem sąsiadujących ścian.

Przykład:

Kątem dwuściennym między ścianami bocznymi ostrosłupa czworokątnego będzie kąt zaznaczony na rysunku poniżej:

Przecięciem ścian jest krawędź boczna. Na obu ścianach zostały wykreślone odcinki prostopadłe do wyróżnionej krawędzi bocznej (są one wysokościami trójkątów będących ścianami bocznymi). Kąt dwuścienny jest kątem pomiędzy tymi odcinkami.